基本思想
并查集是一种维护集合的数据结构,即为 Union(合并)Find(查找)Set(集合)① 合并:合并两个集合。② 查找:判断两个元素是否在一个集合。
如图题目为例:

代码如下:

最小生成树
克鲁斯卡尔算法
一般先选取一点,不断寻找此点旁权数最小的边并连接至对应点,不断重复直至无边。当网的顶点个数较多、而边的条数较少时,使用克鲁斯卡尔算法构造最小生成树效果较好
输入样例
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例
6 自写代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N = 100010, M = 200010, INF = 0x3f3f3f3f;
int n,m;
int p[N];
//排序结构体存边
struct Edge
{
int a,b,w;
bool operator< (const Edge &W)const
{
return w < W.w;
}
}edges[M];
//并查集寻根节点
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int kruskal()
{
//排序
sort(edges, edges + m);
//初始化
for(int i = 1; i <= n; i++) p[i] = i;
//res存所有边的总长,cnt记边
int res = 0, cnt = 0;
for(int i = 0; i < m; i++)
{
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
//a的根节点不等于b的根节点,说明未加入到连通块
if(a!=b)
{
p[a] = b;
res += w;
cnt ++;
}
}
if(cnt < n-1) return INF;
return res;
}
int main()
{
scanf("%d%d", &n, &m);
//存边
for(int i = 0; i < m; i++)
{
int a,b,w;
scanf("%d%d%d", &a, &b, &w);
edges[i] = {a,b,w};
}
int t = kruskal();
if(t == INF) puts("impossible");
else printf("%d\n", t);
return 0;
} 普里姆算法
代码如下:
#include<bits/stdc++.h>
using namespace std;
int g[100][100],m,n,u,v,w;
int f[100],q[1000],mi;
bool vis[100000];
void prim()
{
for(int i=1;i<=n-1;i++)
{
int mn=0x3f3f3f3f;
for(int j=1;j<=n;j++)
{
if(!vis[j]&&mn>f[j])
{
mn=f[j];
mi=j;
}
}
vis[mi]=true;
for(int j=1;j<=n;j++)
{
if(!vis[j]&&g[mi][j]<f[j])
{
f[j]=g[mi][j];
q[j]=mi;
}
}
}
int sum=0;
for(int i=1;i<=n;i++)
{
sum+=f[i];
}
cout<<sum<<endl;
}
int main()
{
freopen(“prim.in”,”r”,stdin);
cin>>m>>n;
memset(g,0x3f3f3f,sizeof(g));
for(int i=1;i<=m;i++)
{
cin>>u>>v>>w;
g[u][v]=w;
g[v][u]=w;
}
for(int i=1;i<=n;i++)
g[i][i]=0;
for(int i=1;i<=n;i++)
{
f[i]=g[1][i];
q[i]=1;
}
vis[1]=true;
prim();
return 0;
}基本方法
1).输入:一个加权连通图,其中顶点集合为V,边集合为E;
2).初始化:Vnew = {x},其中x为集合V中的任一节点(起始点),Enew = {},为空;
3).重复下列操作,直到Vnew = V:
a.在集合E中选取权值最小的边<u, v>,其中u为集合Vnew中的元素,而v不在Vnew集合当中,并且v∈V(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一);
b.将v加入集合Vnew中,将<u, v>边加入集合Enew中;
4).输出:使用集合Vnew和Enew来描述所得到的最小生成树。
| 图例 | 说明 | 不 可 选 | 可 选 | 已 选 |
 | 原始的加权连通图 | |||
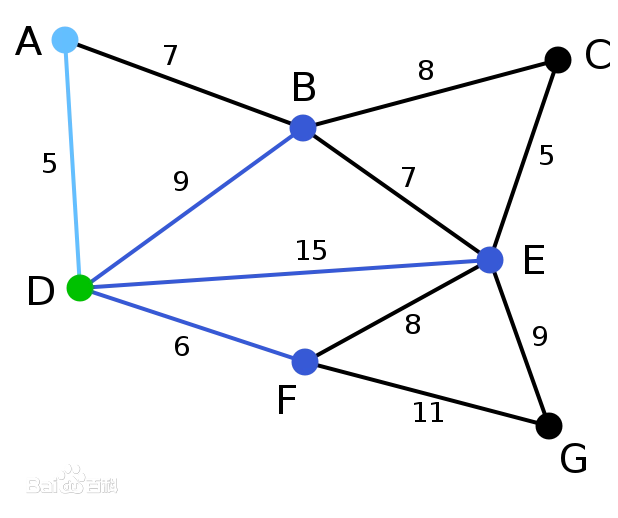 | 顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点,因此将A及对应边AD以高亮表示。 | C, G | A, B, E, F | D |
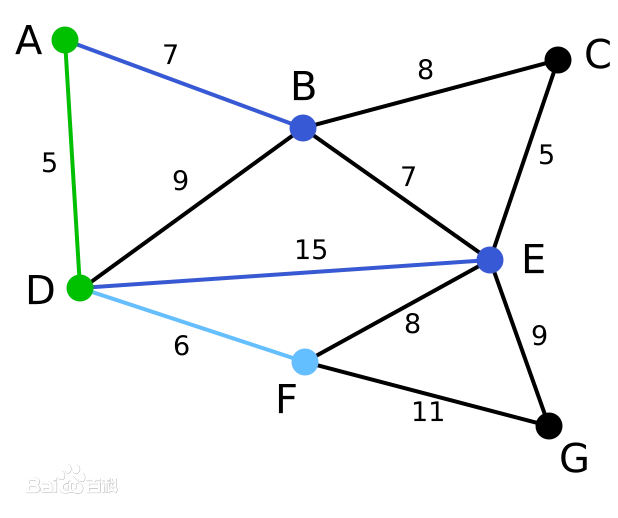 | 下一个顶点为距离D或A最近的顶点。B距D为9,距A为7,E为15,F为6。因此,F距D或A最近,因此将顶点F与相应边DF以高亮表示。 | C, G | B, E, F | A, D |
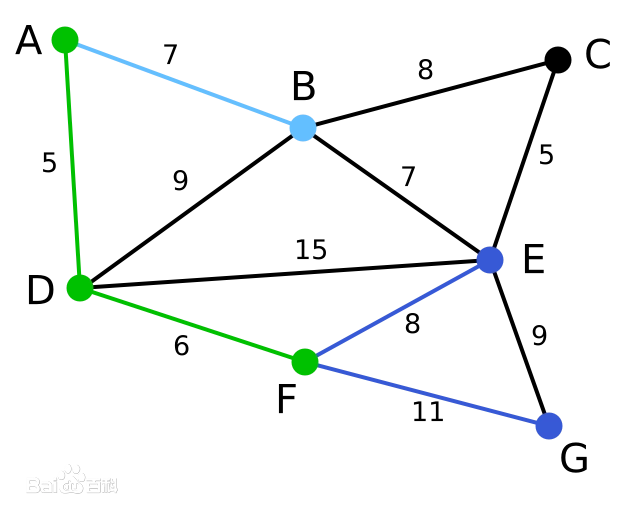 | 算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。 | C | B, E, G | A, D, F |
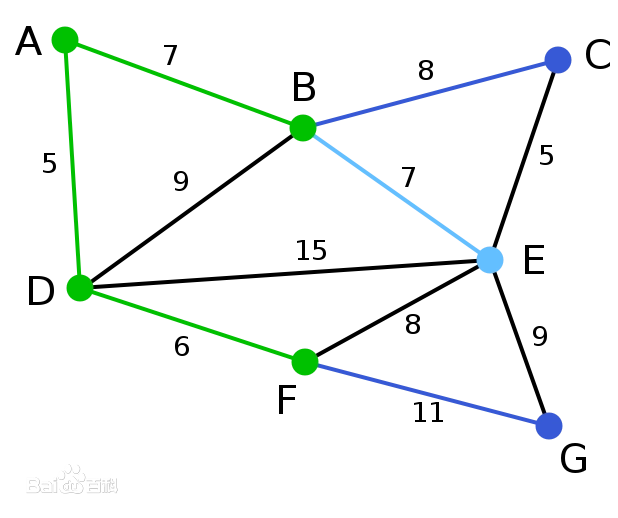 | 在当前情况下,可以在C、E与G间进行选择。C距B为8,E距B为7,G距F为11。点E最近,因此将顶点E与相应边BE高亮表示。 | C, E, G | A, D, F, B | |
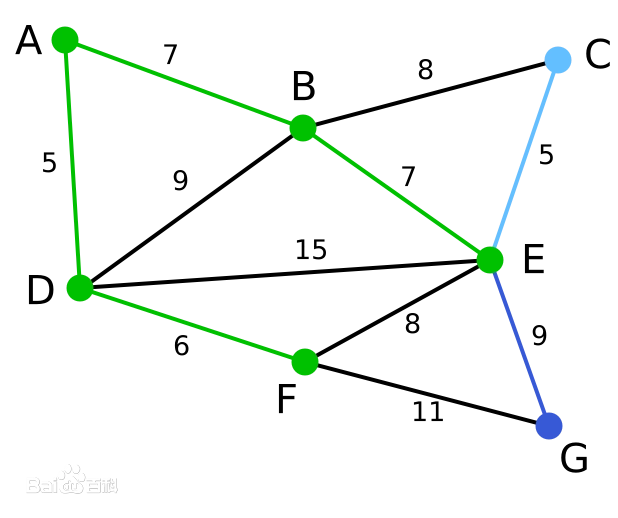 | 这里,可供选择的顶点只有C和G。C距E为5,G距E为9,故选取C,并与边EC一同高亮表示。 | C, G | A, D, F, B, E | |
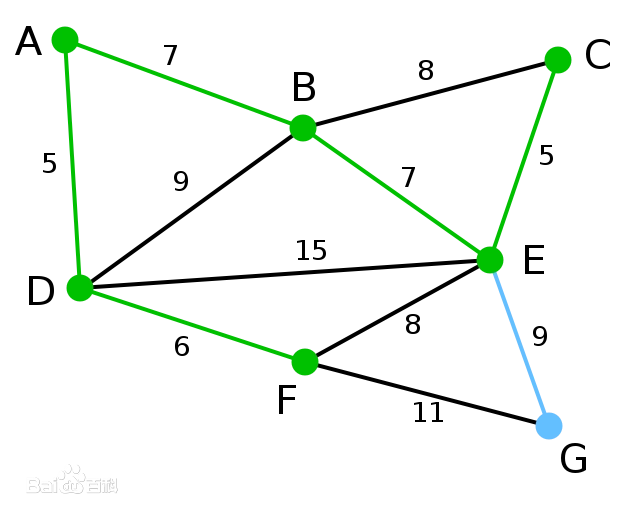 | 顶点G是唯一剩下的顶点,它距F为11,距E为9,E最近,故高亮表示G及相应边EG | G | A, D, F, B, E, C | |
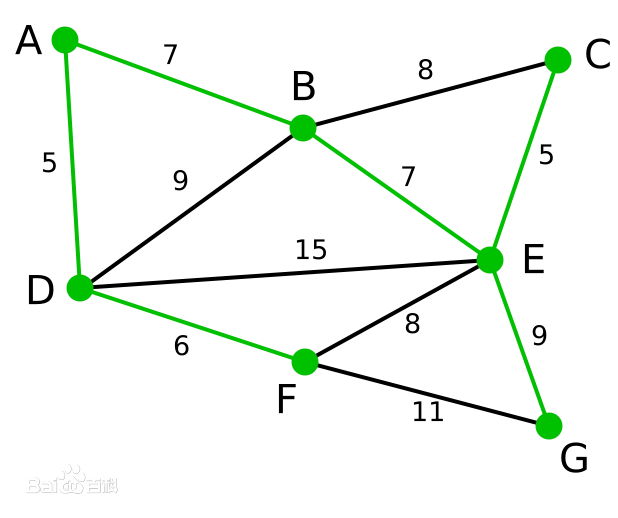 | 所有顶点均已被选取,图中绿色部分即为连通图的最小生成树。在此例中,最小生成树的权值之和为39。 | A, D, F, B, E, C, G |
